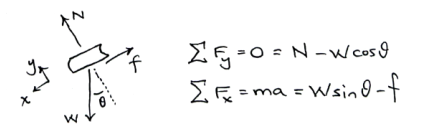
There are a lot of difficult problems to solve in this course, so
students sensibly use the most practical and familiar methods to do it.
This often involves carrying numbers throughout a long solution. The
following scenario illustrates the advantages of using symbols
(variables) rather than numbers.
Alice and Bob, both good students, have different ways of solving
Physics problems. Let’s compare their approaches as they confront the
problem shown below.
They both begin with a free body diagram and Newton’s 2nd Law.
But from this point Alice proceeds symbolically while Bob sticks with
numerical values.
They both got the right answer, but there are several important
differences.
- Alice is done sooner, spending much less time at
her calculator.
- Alice is less likely to make a mistake. On each
line it’s easy to check her algebra. She may use dimensional analysis as an additional quick
check. For example when she finds acceleration, it reasonably appears to
be a dimensionless factor times \(g\).
Bob had to carefully copy each number from his calculator, potentially
introducing a hidden error, and he cannot check his result without
re-doing it.
- Alice understands more. She sees that book’s mass
doesn’t matter -– the answer applies to any mass. She sees that if \(\mu=0\) (frictionless ramp) then \(v=\sqrt{2gh}\), which she might recognize
as the velocity after free-fall. She notices the interesting fact that
the analysis fails when \(\mu>\tan
\theta\) (not steep enough to slide). She can see relationships
like the fact that a ramp of twice the height would yield a velocity
only \(\sqrt{2}\) times faster. If she
wanted she could produce a graph of final speed vs. ramp angle. Bob,
unfortunately, can do none of these things.
- If the final answer were incorrect, Alice would have a much easier
time finding errors. Anyone could quickly scan her
solution for misapplied theory or algebra mistake, but would have to
walk through every step of Bob’s work with a calculator.
- Alice’s symbolic solution works with any unit
system. Her final equation is true in metric or imperial or any
other units. For Alice, units only appear on the last line as she goes
to the calculator. Bob has to make sure his units are right at every
step.
- Alice can go back later and understand what she
did. All her equations are there to see. She might be able to re-use one
of her intermediate results in a later problem, or use this work to
study from.
- Even though Bob kept four significant digits, round-off
error has accumulated in his solution. His answer is incorrect
in the third digit. This would be greater problem if he kept only 3
digits, or if the problem had more steps, or if an intermediate result
were squared or exponentiated, which compounds the error.
- If Alice wanted to compare solutions with another
student who was given \(\mu=0.7\), she
could easily do so. Bob would have to re-do the entire problem.
- Alice’s algebra skills get stronger with each
problem. Poor Bob develops tendinitis in his calculator finger.
Of course the method you use is up to you. Some combination of
numerical and symbolic work may suit you best.
If you use the symbolic approach, you might consider these tips:
- Assign symbols to input data, including units. Then use these
symbols in your solution.
- If the equations get complicated, define intermediate variables for
expressions that keep reappearing. Pro tip: if the variables you define
are dimensionless, your equations will be easier to check and
their physical meaning will often be clearer.
- As you work, keep track of which variables have known values and
which are still unknown.
- Use a computer to do the calculating. For example, write up the
symbolic solution in a Jupyter
Notebook. Save the code for double-checking, re-use and
sharing.
Last modified: March 30, 2025